Linear Elastic Mechanics of Mock Arteries: Empirical Versus …
Mock Artery Compliance
by | RMBS 2007 | Publications, Compliance, High Speed Photography, Silicone Mock Arteries
Linear Elastic Mechanics of Mock Arteries: Empirical Versus Theoretically Predicted Pulsatile Stent Deflection
Biomedical Science Instrumentation, 43, pp. 54-62, (2007)
Ramesh Rajesh1, Conti JC2, Strope ER1
1 Dynatek dalta Scientific Instruments, 105 E Fourth St, Galena, MO 65656
2 Department of Physics, Astronomy and Material Sciences, Missouri State University, Springfield, MO 65803
RMBS 2007
Abstract
Evaluation of a medical device requires human or animal studies to be conducted. In the past decade, the use of mock arteries or mock vessels has found its place in the cardiovascular industry as a best alternative to researchers. Mechanical characteristics of the mock artery play a significant role on the stent and vascular grafts being tested. It is these mechanical characteristics that determine the amount of load applied on the medical device thus deciding the validity of the fatigue test on the devices. This paper is an effort towards determining the distension of the mock artery and relating it to the distension of the vascular stent.
Keywords
linear elastic mechanics, stent durability, deflection, pulsatile, accelerated, mock artery, high speed photography, laser micrometry
Introduction
In the fatigue testing of medical devices like stents and grafts, the amount of load applied to the devices plays a very important role in determining the effectiveness of the durability testing. The load applied by and to the mock vessel is interpreted in terms of distension of the mock vessel. Depending on the location of measurement (outer diameter or inner diameter), this distension of the mock vessel varies based on linear mechanics of the mock arteries. This research work was conducted to make a comparison of distension measured at the outer periphery and inner periphery of the mock arteries and also how the distension of the mock artery is related to the distension of the medical device. In this study a silicone mock artery with a stent deployed within it was tested at different frequencies: 72, 600 and 1800 bpm.
Methods
A silicone mock artery (OD=24.94mm, ID=21.20mm, length=12.5cm) with a stent deployed inside was used in this study. All of the initial dimensional measurements of the mock artery were done using a LaserMike 183 (LaserMike, Dayton, OH). The silicone mock artery along with the stent was tested in a dynamic internal compliance tester (DCT2) for radial compliance (Dynamic Compliance Tester Model DCT2, Dynatek Dalta Scientific Instruments, Galena, MO). The DCT2 was used to create the distension of the mock artery along with the stent in it as a whole unit. During this testing, a high speed photographic camera (Fast Cam PCI 1280 Camera with Photron Motion Tools Software Version 1.05, Motion Engineering, Indianapolis, IN) was used to measure the distension of the stent directly. Simultaneously, a laser micrometer (Laser Micrometer LS7600, Keyence Corp, Woodcliff Lake, NJ) was used to measure the distension of the outside diameter of the tube directly, and this data was used with linear elastic mechanics equations to indirectly predict the distention of the inside diameter of the tube. Since it is known [3,8] that the compliance or distension characteristics of the mock artery changes with the testing frequency, this mock artery was tested at three different frequencies, 72 bpm, 600 bpm and 1800 bpm. During this testing, the pressure in the mock artery was pulsed from 0 to approximately 140mm Hg.
The high speed photographic camera was also used to measure the distension of the outer diameter of the mock artery directly around the stent. This was achieved by camera tracking the markings 12.10mm apart on the outer diameter of the mock artery. The distension of the outer diameter of the mock artery along with linear elastic mechanics equations was used to predict the distension of the inner diameter. This, along with the high speed photographic analysis of the stent, will test the hypothesis that one can predict the distension of the stent under test by measuring the distension of the outer diameter of the tube and converting it to inner diameter distension.
The laser micrometer was used to monitor the distension of the outer diameter of the mock artery. This distension of the mock artery directly around the stent along with linear elastic mechanics equations was used in calculating the distension of the inner diameter.
Measurements using the Dynamic Compliance Tester (DCT2):
The dynamic internal compliance tester is equipped with a speed controlled DC motor. This motor turns a shaft that is in conjunction with an adjustable eccentric coupler. This coupler along with a crank arm converts the rotational motion into linear motion. This linear motion is used to move a drive rod, which in turn compresses a bellows. During the test setup, the mock artery is fixed in the DCT2 machine such that one end is attached to the discharge end of the bellows and the other end is fixed to a manifold to which a pressure transducer is attached.
The basic principle for compliance measurement using a DCT2 machine is as follows: A highly sensitive linear voltage to displacement transducer (LVDT) monitors the position of the drive rod, which in turn is interpreted in terms of the amount of fluid injected from the bellows. Pressure is monitored by the pressure transducer and length change is monitored but neglected since the mock artery is fixed under slight tension between the two ports. All test data are acquired and recorded on a computer using a LabView (National Instruments, Austin, TX) data acquisition system. Data obtained from the DCT2 (pressure and change in volume) are used to plot a graph of loading and unloading curves. A second order polynomial curve is used to define a curve of best fit. To determine the radial compliance of the tube (mock artery), the initial length (Li) and initial radius (Ri) of the tube is measured, resulting in the initial volume (Vi) of the tube as follows: [7]
Vi = Π ×Ri2 ×Li
Vi is the volume at 0 mm Hg pressure.
If the tube is then inflated to a new pressure P2 with the length being fixed (there is no change in length Li), a new set of dimensions results for the tube depending on its compliance. Let ∆V be the change in volume. Therefore the final volume Vf of the tube at pressure P2 is given by:
Vf = Vi +∆ V
Vf = Π × Rf2×Li (where Rf is the radius at pressure P2)
Rf = sqrt (Vf / (Π ×Li))
% radial compliance (per 100mm Hg) is given by ((Rf-Ri) / (Ri × ∆P)) × 104
where ∆ P is change in pressure expressed in mm Hg.
Distension measurement using high speed photography [8-10]:
A high speed photographic camera was used to determine the distension of the mock artery with the stent deployed inside. The camera’s associated tracking software has the capability of analyzing the fast motion within the captured image. The basic principle for distension measurements using high speed photography is as follows: The high speed camera will track the markings placed on the diameter of the mock arteries. The relative distance between these markings changes as the tube expands. The percent change in the chord length will be the same percentage change that occurs in the diameter and circumference.
Let us assume the cross section of the mock artery to be a circle of radius ri with center O.
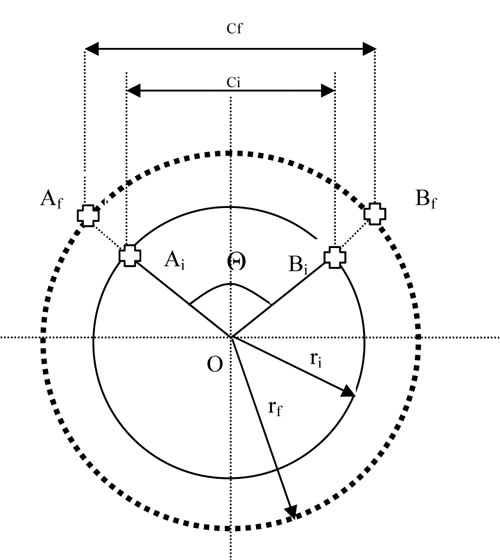
Fig 1: Schematic Representation of Mock Artery
Select two points Ai and Bi on the circle such that the arc AiBi subtends an angle Θ at the center of the circle as shown in the Fig 1. Let ci be the initial length of the chord AiBi.
So:
Ci = 2 sin (Θ/2) ri
As the mock artery is being pulsed from lower pressure to higher pressure, let Af and Bf be the final positions of points Ai and Bi respectively and rf be the final radius. Let the distance between Af and Bf be cf. The % strain (%Є) in the chord length is given by change in the chord length divided by the original chord length.
% Є = ((cf-ci)100)/ci
But cf = 2 sin (Θ/2) rf
Therefore, % Є =(rf – ri)/ ri
Distension measurement using laser micrometer:
A laser micrometer was used for measuring external distension of the mock artery due to change in pressure. The LS7600 Digital Micrometer used for this experiment has a repeatable accuracy of ±3µm and high sampling rate of 2400 scans per second. The basic principle of distension measurement using a laser micrometer is as follows: Let Di be the external diameter of the mock artery measured at 0 mm Hg pressure. The mock artery is then inflated to a new pressure P2 with the length being fixed, and Df is the diameter at the inflated pressure. Then the % distension of the mock artery is given by: ((Df – Di)/ Di) ×100
Theoretical measurement:
The relationship between the inner and outer tube diameters based on linear elastic mechanics is used in calculating the one when the other is measured. The equation used in this research work is:
Di2= {b+ [(1+a2/b2)- ν (1-a2/b2 + 2ν)] [b Δa/a]} [7]
2(1-ν2)
where: Di2 is the pressurized inner diameter;
ν is Poisson’s ratio (for silicone= 0.41)
a is the initial outer diameter (in mm)
b is the initial inner diameter (21.20mm)
Δa is the change in outer diameter due to change in pressure
In this equation the values for the change in outer diameter Δa was obtained from both high speed photography and laser micrometer measurements.
Results
The DCT2 measured the change in internal diameter with respect to change in internal pressure. This change in internal diameter was used to calculate the percentage change in distension of the inner wall of the mock artery. Table 1 shows the results from the DCT2.
Table 1: Tube ID Distensions by Dynamic Compliance Tester
|
Frequency |
Peak |
Initial |
Final |
% Compliance |
% Distension |
|||||
| 72 | 141.00 | 21.20 | 22.63 | 4.80 | 6.77 | |||||
| 72 | 140.00 | 21.20 | 22.63 | 4.82 | 6.75 | |||||
| 72 | 140.00 | 21.20 | 22.61 | 4.76 | 6.66 | |||||
| 600 | 143.00 | 21.20 | 22.36 | 3.83 | 5.48 | |||||
| 600 | 142.00 | 21.20 | 22.35 | 3.81 | 5.41 | |||||
| 600 | 145.00 | 21.20 | 22.37 | 3.81 | 5.52 | |||||
| 1800 | 149.00 | 21.20 | 21.73 | 1.67 | 2.49 | |||||
| 1800 | 154.00 | 21.20 | 21.72 | 1.60 | 2.46 | |||||
| 1800 | 152.00 | 21.20 | 21.72 | 1.62 | 2.46 |
The two markings on the outer diameter of the mock artery were tracked using the automated tracking function provided by the Photron motion Software and the data points were exported to a spreadsheet. Strain in the chord length was measured and percentage of distension of the outer diameter was calculated as shown in Table 2. Two points were also picked on the stent deployed inside the mock artery. These two points were also tracked for distension in the stent.
Table 2: Tube OD Distensions and Stent Diameter using H.S. Camera
|
Frequency |
Peak |
Final Outer Diameter (mm) | % Outer Distension |
% |
||||
| 72 | 141.00 | 26.14 | 4.85 | 1.75 | ||||
| 72 | 140.00 | 26.07 | 4.54 | 1.69 | ||||
| 72 | 140.00 | 26.13 | 4.78 | 1.61 | ||||
| 600 | 143.00 | 25.96 | 4.35 | 1.91 | ||||
| 600 | 142.00 | 26.01 | 4.30 | 1.88 | ||||
| 600 | 145.00 | 26.04 | 4.40 | 1.92 | ||||
| 1800 | 149.00 | 25.57 | 2.54 | 2.30 | ||||
| 1800 | 154.00 | 25.49 | 2.20 | 2.16 | ||||
| 1800 | 152.00 | 25.49 | 2.19 | 2.08 |
The outer diameter measurement was used along with the linear elastic mechanics equation in calculating the pressurized inner diameter of the mock artery and tabulated as shown in Table 3.
Table 3: Calculated Tube % ID Distension Using H.S. Camera Measurements
and LEM Equations
|
Frequency |
Peak |
Initial |
Change |
Final |
Initial |
% |
||||||
| 72 | 141.00 | 24.94 | 1.20 | 22.54 | 21.20 | 6.34 | ||||||
| 72 | 140.00 | 24.94 | 1.13 | 22.47 | 21.20 | 6.00 | ||||||
| 72 | 140.00 | 24.94 | 1.19 | 22.54 | 21.20 | 6.31 | ||||||
| 600 | 143.00 | 24.94 | 1.02 | 22.34 | 21.20 | 5.38 | ||||||
| 600 | 142.00 | 24.94 | 1.07 | 22.40 | 21.20 | 5.68 | ||||||
| 600 | 145.00 | 24.94 | 1.10 | 22.43 | 21.20 | 5.81 | ||||||
| 1800 | 149.00 | 24.94 | 0.63 | 21.91 | 21.20 | 3.35 | ||||||
| 1800 | 154.00 | 24.94 | 0.55 | 21.82 | 21.20 | 2.91 | ||||||
| 1800 | 152.00 | 24.94 | 0.55 | 21.81 | 21.20 | 2.89 |
The change in external diameter due to change in internal pressure was monitored by Laser micrometer and thus the external distension was calculated and tabulated as shown in Table 4.
Table 4: OD Distension by Laser Micrometer
|
Frequency |
Peak |
Final |
Initial |
% Outer |
||||
| 72 | 141.00 | 26.39 | 24.95 | 5.77 | ||||
| 72 | 140.00 | 26.39 | 24.95 | 5.79 | ||||
| 72 | 140.00 | 26.39 | 24.96 | 5.77 | ||||
| 600 | 143.00 | 26.36 | 25.09 | 5.10 | ||||
| 600 | 142.00 | 26.36 | 25.07 | 5.13 | ||||
| 600 | 145.00 | 26.36 | 25.07 | 5.14 | ||||
| 1800 | 149.00 | 26.18 | 25.36 | 3.22 | ||||
| 1800 | 154.00 | 26.09 | 25.28 | 3.21 | ||||
| 1800 | 152.00 | 26.19 | 25.36 | 3.27 |
The outer diameter measurement was used along with the linear elastic mechanics equation in calculating the pressurized inner diameter of the mock artery and tabulated as shown in Table 5.
Table 5: Inner Distension of the Mock Artery Using Linear Elastic Mechanics Equations and Laser Outside Diameter Measurements
| Frequency (Hz) |
Peak Pressure (mm Hg) |
Initial Outer Diameter (mm) |
Change in Outer Diameter Δ a(mm) |
Final Inner Diameter using Calculations (mm) |
Initial Inner Diameter (mm) |
% Inner Distension |
||||||
| 72 | 141.00 | 24.95 | 1.44 | 22.82 | 21.20 | 7.63 | ||||||
| 72 | 140.00 | 24.95 | 1.44 | 22.82 | 21.20 | 7.65 | ||||||
| 72 | 140.00 | 24.96 | 1.44 | 22.82 | 21.20 | 7.62 | ||||||
| 600 | 143.00 | 25.09 | 1.28 | 22.64 | 21.20 | 6.77 | ||||||
| 600 | 142.00 | 25.07 | 1.29 | 22.65 | 21.20 | 6.82 | ||||||
| 600 | 145.00 | 25.07 | 1.29 | 22.65 | 21.20 | 6.83 | ||||||
| 1800 | 149.00 | 25.36 | 0.82 | 22.12 | 21.20 | 4.33 | ||||||
| 1800 | 154.00 | 25.28 | 0.81 | 22.11 | 21.20 | 4.30 | ||||||
| 1800 | 152.00 | 25.36 | 0.83 | 22.13 | 21.20 | 4.39 |
Discussion
The purpose of this set of experiments was to evaluate whether or not an investigator could predict pulsatile stent distensions during performance or durability testing. A review of the data reveals several things (Tables 1-6 and Figure 1). First, the final outer diameter as measured by the laser method was consistently 0.3 to 0.5mm greater than that measured by the camera method. This could be due to a calibration error. Second, this difference manifests itself in a 0.8 to 1.0% greater pulsatile distension when measured by the laser. Third, in all cases, compliance and distension of the mock artery reduces with increased frequency. This is a well-known phenomenon. [3,8] Fourth, in all cases the distension of the stent is less than the distension of the mock artery inner diameter. Last, but most surprising, the distension of the stent increases with increasing frequency. This increase could be due to the gradual approach of the frequency of the test to a harmonic of the stent.
Clearly, measuring the outside diameter of the mock artery and calculating the pulsatile distension of the inner diameter cannot predict the motion of the stent.
There is the possibility, however, of developing a correlation between camera-measured stent distension and laser-measured mock artery outside diameter distension to allow the laser to monitor properly set up experiments.
Table 6: Method Comparison of Mock Vessel ID and Stent Distensions in % Change.
| Frequency (Hz) |
Tube ID Distensions using DCT | Tube ID Distensions using H.S. Camera OD and LEM EQ | Tube ID Distensions using Laser OD and LEM EQ | H.S. Camera Distension of Stent Directly | ||||
| 72 | 6.73 ± 0.06 | 6.24 ± 0.21 | 7.64 ± 0.01 | 1.68 ± 0.07 | ||||
| 600 | 5.47 ± 0.06 | 5.75 ± 0.07 | 6.81 ± 0.03 | 1.90 ± 0.02 | ||||
| 1800 | 2.47 ± 0.01 | 3.05 ± 0.26 | 4.34 ± 0.04 | 2.18 ± 0.11 |
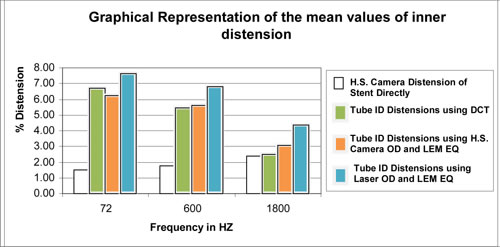
Figure 1
Acknowledgement
Special thanks to all employees of Dynatek dalta Scientific Instruments.
References
1 ) Conti, J.C., Strope, E.R., Price, K.S., Goldenberg, L.M, The High Frequency Testing of Vascular Grafts and Vascular Stents: Influence of Sample Dimensions on Maximum Allowable Frequency, Biomedical Sciences Instrumentation, 35, 339-346 (1999)
2 ) Conti, J.C. and Strope, E.R., Radial Compliance of Natural and Mock Arteries: How this Property Defines the Cyclic Loading of Deployed Vascular Stents. Biomedical Sciences Instrumentation, 38, 163-171 (2002)
3 ) Conti, J.C., Strope, E.R., Rhode, D.J. and Spence, L.D., Frequency Dependent Radial Compliance of Latex Tubing, Biomedical Sciences Instrumentation, 33, 524-529 (1997)
4 ) Conti, J.C., Strope, E.R., Rohde, D.R. and Greisler, H.P., A New Technique to Determine Vascular Compliance In Vivo, National Heart Lung and Blood Institute Contractors Meeting, Louisville, KY, 1989
5 ) Conti, J.C., Strope, E.R., Price K.S, Sources of Error in Monitoring High Speed Testing of Vascular Grafts, Biomedical Sciences Instrumentation, 34, 240-245 (1998)
6 ) Gonza, E.R., Mason, W.F., Marble, A.E., and others, Necessity for Elastic Properties in Synthetic Arterial Grafts, Can. J. Surg., 17, 176-179 (1974)
7 ) AAMI/ISO standard ISO/CD- V-1 25539-01:2003 and ANSI/AAMI VP-20, 1994
8 ) Ramesh, R., Strope E.R., Price K.S., Conti J.C., Frequency Dependent Hysteresis of Silicone and Latex Mock Arteries Used in Stent Testing, Biomedical Sciences Instrumentation, 41, 163-168 (2005)
9 ) Kattekola, B., Conti J.C., Strope E.R., High Speed Photographic Verification of Intravascular Stent Strains During Accelerated Durability Testing, Biomedical Sciences Instrumentation, 40, 219-224 (2004)
10 ) Ramesh R. , Conti J.C., Strope E.R., Single Versus Double Ended High Frequency Pressurization of Mock Arteries: Symmetry of Expansion, Biomedical Sciences Instrumentation, 41, 446-451 (2006)



